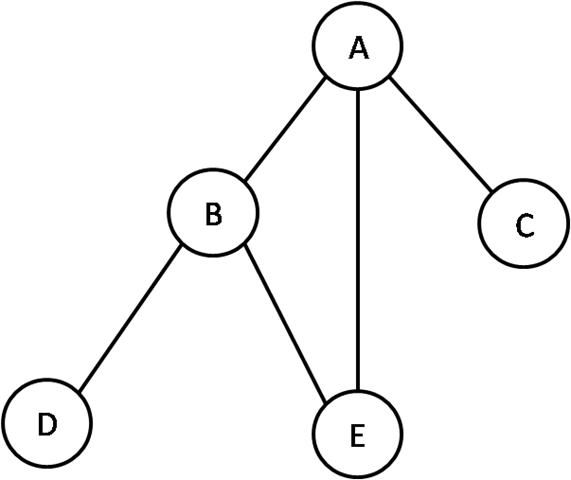
Graphs are useful tools for visualizing or representing real world problems, but in order to use graphs for computing problems, we need to represent a graph in a programming paradigm. The most common form of representing a graph in programming terms is using adjacency matrices. Consider this simple non directed graph.
we can represent the vertices and edges using a 2 dimensional Boolean array.
As we have 5 vertices in the above graph namely A,B,C,D and E
the array will be a 5x5 matrix.
lets initialize the array as:
boolean arr[5][5];
let us assume i and j as the starting and ending vertex.
if arr[i][j]=true, that means there is a connection from i to j.
as it is a non directed graph we assume that
if arr[i][j]=true then arr[j][i] is also true;
the matrix for the above graph will look like this:
int arr[5][5]= {{0,1,1,0,1},
{1,0,0,1,1},
{1,0,0,0,0},
{0,1,0,0,0},
{1,1,0,0,0}}
This is how different types of graphs are represented using an adjacency matrix. Once we are able to represent a graph in a matrix format, the programming part becomes easy. Once we have the adjacency matrix we can apply different algorithms to identify the properties of a given graph.
we can represent the vertices and edges using a 2 dimensional Boolean array.
As we have 5 vertices in the above graph namely A,B,C,D and E
the array will be a 5x5 matrix.
lets initialize the array as:
boolean arr[5][5];
let us assume i and j as the starting and ending vertex.
if arr[i][j]=true, that means there is a connection from i to j.
as it is a non directed graph we assume that
if arr[i][j]=true then arr[j][i] is also true;
the matrix for the above graph will look like this:
A B C D E
A 0 1 1 0 1
B 1 0 0 1 1
C 1 0 0 0 0
D 0 1 0 0 0
E 1 1 0 0 0
So the array can be initialized as:
int arr[5][5]= {{0,1,1,0,1},
{1,0,0,1,1},
{1,0,0,0,0},
{0,1,0,0,0},
{1,1,0,0,0}}
Similarly a weighted and or directed graph can also be represented in a similar manner, but the difference is that instead of Boolean values, the matrix will hold the weights. lets take an example to explain how a directed and weighted graph can be represented using adjacency matrix.
The adjacency matrix for the above graph will look like this
Bob Alice Charlie
Bob 0 0 10
Alice 20 0 5
Charlie 0 0 0
So the array can be initialized as:
int arr[3][3]= {{0,0,10},
{20,0,5},
{0,0,0}}
The adjacency matrix for the above graph will look like this
Bob Alice Charlie
Bob 0 0 10
Alice 20 0 5
Charlie 0 0 0
So the array can be initialized as:
int arr[3][3]= {{0,0,10},
{20,0,5},
{0,0,0}}
This is how different types of graphs are represented using an adjacency matrix. Once we are able to represent a graph in a matrix format, the programming part becomes easy. Once we have the adjacency matrix we can apply different algorithms to identify the properties of a given graph.